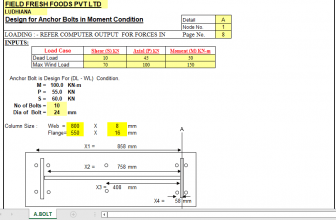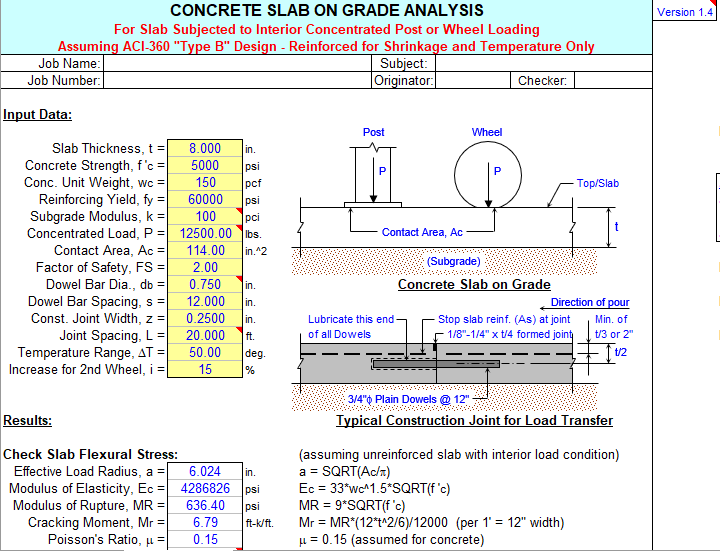
“GRDSLAB” — CONCRETE SLAB ON GRADE ANALYSIS
Program Description:
“GRDSLAB” is a spreadsheet program written in MS-Excel for the purpose of analysis of concrete slabs on
grade. Specifically, a concrete slab on grade may be subjected to concentrated post or wheel loading. Then
for the given parameters, the slab flexural, bearing, and shear stresses are checked, the estimated crack width is
determined, the minimum required distribution reinforcing is determined, and the bearing stress on the dowels
at construction joints is checked. Also, design charts from the Portland Cement Association (PCA) are included
to provide an additional method for determining/checking required slab thickness for flexure. The ability to
analyze the capacity of a slab on grade subjected to continuous wall (line-type) load as well as stationary,
uniformly distributed live loads is also provided.
This program is a workbook consisting of eight (8) worksheets, described as follows:
Worksheet Name Description
Doc This documentation sheet
Slab on Grade Concrete Slab on Grade Analysis for Concentrated Post or Wheel Loading
PCA Fig. 3-Wheel Load PCA Figure 3 – Design Chart for Single Wheel Loads
PCA Fig. 7a-Post Load PCA Figure 7a – Design Chart for Post Loads (k = 50 pci)
PCA Fig. 7b-Post Load PCA Figure 7b – Design Chart for Post Loads (k = 100 pci)
PCA Fig. 7c-Post Load PCA Figure 7c – Design Chart for Post Loads (k = 200 pci)
Wall Load Concrete Slab on Grade Analysis for Wall Load
Unif. Load Concrete Slab on Grade Analysis for Stationary Uniform Live Loads
Program Assumptions and Limitations:
- This program is based on the following references:
a. “Load Testing of Instumented Pavement Sections – Improved Techniques for Appling the Finite Element
Method to Strain Predition in PCC Pavement Structures” – by University of Minnesota, Department of Civil
Engineering (submitted to MN/DOT, March 24, 2002)
b. “Principles of Pavement Design” – by E.J. Yoder and M.W. Witczak (John Wiley & Sons, 1975)
c. “Design of Concrete Structures” – by Winter, Urquhart, O’Rourke, and Nilson” – (McGraw-Hill, 1962)
d. “Dowel Bar Opimization: Phases I and II – Final Report” – by Max L. Porter (Iowa State University, 2001)
e. “Design of Slabs on Grade” – ACI 360R-92 – by American Concrete Institute (from ACI Manual of Concrete
Practice, 1999)
f. “Slab Thickness Design for Industrial Concrete Floors on Grade” (IS195.01D) – by Robert G. Packard
(Portland Cement Association, 1976)
g. “Concrete Floor Slabs on Grade Subjected to Heavy Loads”
Army Technical Manual TM 5-809-12, Air Force Manual AFM 88-3, Chapter 15 (1987) - The “Slab on Grade” worksheet assumes a structurally unreinforced slab, ACI-360 “Type B”, reinforced only
for shrinkage and temperature. An interior load condition is assumed for flexural analysis. That is, the
concentrated post or wheel load is assumed to be well away from a “free” slab edge or corner. The original
theory and equations by H.M. Westergaard (1926) as modified by Reference (a) in item #1 above are used for
the flexual stress analysis. Some of the more significant simplifying assumptions made in the Westergaard
analysis model are as follows:
a. Slab acts as a homogenous, isotropic elastic solid in equilibrium, with no discontinuities.
b. Slab is of uniform thickness, and the neutral axis is at mid-depth.
c. All forces act normal to the surface (shear and friction forces are assumed to be negligible).
d. Deformation within the elements, normal to slab surface, are considered.
e. Shear deformation is negligible.
f. Slab is considered infinite for center loading and semi-infinite for edge loading.
g. Load at interior and corner of slab distributed uniformly of a circular contact area.
h. Full contact (support) between the slab and foundation. - Other basic assumptions used in the flexural analysis of the “Slab on Grade” worksheet are as follows:
a. Slab viewed as a plate on a liquid foundation with full subgrade contact (subgrade modeled as a series
of independent springs – also known as “Winkler” foundation.)
b. Modulus of subgrade reaction (“k”) is used to represent the subgrade.
c. Slab is considered as unreinforced concrete beam, so that any contribution made to flexural strength by
the inclusion of distribution reinforcement is neglected.
d. Combination of flexural and direct tensile stresses will result in transverse and longitudinal cracks.
e. Supporting subbase and/or subgrade act as elastic material, regaining position after application of load. - The “Slab on Grade” worksheet allows the user to account for the effect of an additional post or wheel load.
The increase in stress, ‘i’, due to a 2nd wheel (or post) load expressed as a percentage of stress for a single
wheel (or post) load generally varies between 15% to 30% as is to be input by the user. - All four (4) worksheets pertaining to the PCA Figures 3, 7a, 7b, and 7c from Reference (f) in item #1 above are
based on interior load condition and other similar assumptions used in the “Slab on Grade” worksheet.
Other assumed values used in the development of the Figures 3, 7a, 7b, and 7c are as follows:
a. Modulus of elasticity for concrete, Ec = 4,000,000 psi.
b. Poisson’s Ratio for concrete, m = 0.15. - In the four (4) worksheets pertaining to the PCA Figures 3, 7a, 7b, and 7c, the user must manually determine
(read) the required slab thickness from the design chart and must manually input that thickness in the
appropriate cell at the bottom of the page. An interation or two may be required, as when the slab thickness
is input, it may/may not change the effective contact area. Note: the user may unprotect the worksheet (no
password is required) and access the Drawing Toolbar (select: View, Toolbars, and Drawing) to manually
draw in (superimpose) the lines on the chart which are used to determine the required slab thickness. - This program contains numerous “comment boxes” which contain a wide variety of information including
explanations of input or output items, equations used, data tables, etc. (Note: presence of a “comment box”
is denoted by a “red triangle” in the upper right-hand corner of a cell. Merely move the mouse pointer to the
desired cell to view the contents of that particular “comment box”.)