
P-Delta effect P-Delta effect, also known as geometric nonlinearity, involves the equilibrium and compatibility relationships of a structural system loaded about its deflected configuration. Of particular concern is the application of gravity load on laterally displaced multi-story building structures. This condition magnifies story drift and certain mechanical behaviors while reducing deformation capacity. P-Delta effect typically involves large external forces upon relatively small displacements. If deformations become sufficiently large as to break from linear compatibility relationships, then Large-Displacement and Large-Deformation analyses become necessary. The two sources of P-Delta effect are illustrated in Figure 1, and described as follows: P- effect, or P-“small-delta”, is associated with local deformation relative to the element chord between end nodes.
Typically, P- only becomes significant at unreasonably large displacement values, or in especially slender columns. So long as a structure adheres to the slenderness requirements pertinent to earthquake engineering, it is not advisable to model P-, since it may significantly increase computational time without providing the benefit of useful information. An easier way to capture this behavior is to subdivide critical elements into multiple segments, transferring behavior into P- effect (Powell 2006). P- effect, or P-“big-delta”, is associated with displacements relative to member ends. Unlike P-, this type of P-Delta effect is critical to nonlinear modeling and analysis. As indicated intuitively by Figure 2, gravity loading wi ll influence structural response under significant lateral displacement. P- may contribute to loss of lateral resistance, ratcheting of residual deformations, and dynamic instability (Deierlein et al. 2010). As shown in Figure 3, effective lateral stiffness decreases, reducing strength capacity in all phases of the force-deformation relationship (PEER/ATC 2010). To consider P- effect directly, gravity load should be present during nonlinear analysis. Application will cause minimal increase to computational time, and will remain accurate for drift levels up to 10% (Powell 2006). The Types of P-Delta analysis article further explains the difference between P- and P-. Articles Test Problems Title Description Program Interpreting buckling analysis results for different initial conditions Buckling analysis may begin with either zero initial conditions or the stiffness taken from the end of a nonlinear load case. This test problem compares the associated output. SAP2000 P-Delta effect for a cantilevered column Calculation and verification of the P-Delta effects of a cantilevered column. SAP2000 See Also Buckling section References Powell, G. H. (2010). Modeling for Structural Analysis: Behavior and Basics (1st ed.). Berkeley, CA: Computers and Structures, Inc. Available for purchase on the CSI Products > page Deierlein, G. G., Reinhorn, A. M., and Willford, M. R. (2010). Nonlinear Structural Analysis For Seismic Design, NEHRP Seismic Design Technical Brief No. 4., NIST GCR 10-917-5. Gaithersburg, MD: National Institute of Standards and Technology. PEER/ATC (2010). Modeling and acceptance criteria for seismic design and analysis of tall buildings, PEER/ATC 72-1 Report. Redwood City, CA: Applied Technology Council.
2. P-Delta analysis parameters Initial P-Delta analysis may be specified in ETABS via Define>P-Delta Options and using either of the following two methods: Non-iterative Based on Mass, in which load is automatically computed from the mass at each level. This is an approximate method which does not require an iterative solution, providing for faster computation. P-Delta is considered by treating the structure as a simplified stick model, a process which is most effective with a single rigid diaphragm at each level. Local buckling is not captured as effectively. The benefit of this non-iterative method is that P-Delta may be considered in load cases which do not specify gravity load. When gravity load is specified, we generally recommend the Iterative Based on Load Cases method. Iterative Based on Load Cases, in which load is computed from a specified combination of static load cases, then known as the P-Delta load combination. This is an iterative method which considers P-Delta on an element-by-element basis. Local buckling is captured more effectively. An example application may be when load includes the dead load case and a fraction of a live load case. When the iterative method is selected, two additional options become available : Convergence Tolerance (Relative), Iteration is used to make sure that equilibrium is achieved at each step of the analysis. Use this parameter to set the relative convergence tolerance that is used to compare the magnitude of force error with the magnitude of the force acting on the structure. Using a smaller value ensures better equilibrium, although the default value is usually adequate. P-Delta Load Combination, in which users may specify the single load combination for the initial P-Delta analysis. For example, suppose that a building code requires the following load combinations: (1) 1.4 dead load (2) 1.2 dead load + 1.6 live load (3) 1.2 dead load + 0.5 live load + 1.3 wind load (4) 1.2 dead load + 0.5 live load – 1.3 wind load (5) 0.9 dead load + 1.3 wind load (6) 0.9 dead load – 1.3 wind load A P-Delta load combination of 1.2 DL + 0.5 LL is typically conservative when considering P-Delta effect due to the overall sway of a structure. Combinations (3) and (4) will accurately capture this effect, while (5) and (6) should be conservative. Combinations (1) and (2) have no lateral load, therefore P-Delta effect should not be of concern. Please notice this is a non-linear static case and should be performed only after the model runs without any numerical issues for simple linear cases and results of basic variables such as deformations are within realistic or expected values. P- effect ETABS may account for P- effect, which is associated with local deformation relative to the chord between member ends. We do not recommend implementing this method because it will significantly increase computational time without providing the benefit of useful information. Instead, P- may be captured through either of the following methods: Apply design factors, which ETABS post-processing assumes to be done. These factors are therefore included in design, when applicable. Divide members into segments (at least two per column), then run each load case separately with a different P-Delta load combination for each. Notes ETABS uses the same stiffness for all static load cases, response-spectrum analysis, and time-history analysis. See Also AISC stability benchmark problems
P Delta Analysis (How to include P-delta effects) | Part 1
P Delta Analysis (How to include P-delta effects) | Part 2




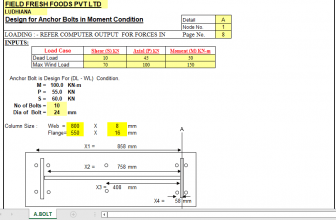

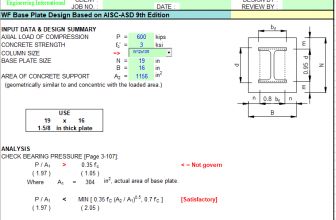
Hi, I have learn a lot from your videos and as you have shown the P-Delta analysis as per American code, I want to know that is there any P-delta in IS code ? or we have to use american code only ?????