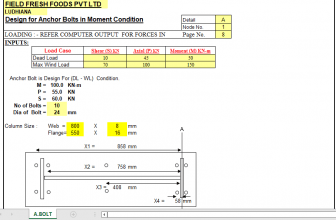
“BEAMANAL” — SINGLE-SPAN and CONTINUOUS-SPAN BEAM ANALYSIS
Program Description:
“BEAMANAL” is a spreadsheet program written in MS-Excel for the purpose of analysis of either single-span or
continuous-span beams subjected to virtually any type of loading configuration. Four (4) types of single-span beams
and two (2) through (5) span, continuous-span beams, considered. Specifically, beam end reactions as well as the
maximum moments and deflections are calculated. Plots of both the shear and moment diagrams are produced,
as well as a tabulation of the shear, moment, slope, and deflection for the beam or each individual span. Also, for
steel single-span beams an AISC 9th Edition (ASD) Code check can be performed for X-axis bending and shear.
This program is a workbook consisting of four (4) worksheets, described as follows:
Worksheet Name Description
Doc This documentation sheet
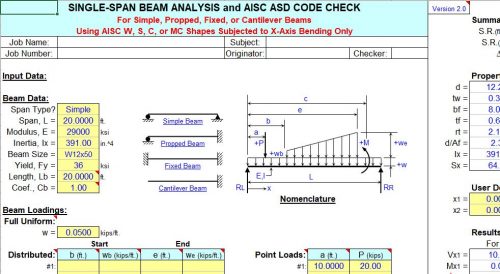
Single-Span Beam Single-span beam analysis for simple, propped, fixed, & cantilever beams
Single-Span Beam & Code Check Single-span beam analysis and AISC Code Check for X-axis bending
Continuous-Span Beam Continuous-span beam analysis for 2 through 5 span beams
Program Assumptions and Limitations:
- The following reference was used in the development of this program (see below):
“Modern Formulas for Statics and Dynamics, A Stress-and-Strain Approach”
by Walter D. Pilkey and Pin Yu Chang, McGraw-Hill Book Company (1978), pages 11 to 21. - This program uses the three (3) following assumptions as a basis for analysis:
a. Beams must be of constant cross section (E and I are constant for entire span length).
b. Deflections must not significantly alter the geometry of the problem.
c. Stress must remain within the “elastic” region. - On the beam or each individual span, this program will handle a full length uniform load and up to eight (8) partial
uniform, triangular, or trapezoidal loads, up to fifteen (15) point loads, and up to four (4) applied moments. - For single-span beams, this program always assumes a particular orientation for two (2) of the the four (4)
different types. Specifically, the fixed end of either a “propped” or “cantilever” beam is always assumed to be on
the right end of the beam. - This program will calculate the beam end vertical reactions and moment reactions (if applicable),
the maximum positive moment and negative moment (if applicable), and the maximum negative deflection
and positive deflection (if applicable). The calculated values for the end reactions and maximum moments
and deflections are determined from dividing the beam into fifty (50) equal segments with fifty-one (51) points,
and including all of the point load and applied moment locations as well. (Note: the actual point of maximum
moment occurs where the shear = 0, or passes through zero, while the actual point of maximum deflection is
where the slope = 0.) - The user is given the ability to input two (2) specific locations from the left end of the beam to calculate the
shear, moment, slope, and deflection. - The user is also given the ability to select an AISC W, S, C, MC, or HSS (rectangular tube) shape to aide in
obtaining the X-axis moment of inertia for input for the purely analysis worksheets. - The plots of the shear and moment diagrams as well as the displayed tabulation of shear, moment, slope,
and deflection are based on the beam (or each individual span) being divided up into fifty (50) equal segments
with fifty-one (51) points. - For continuous-span beam of from two (2) through five (5) spans, this program utilizes the “Three-Moment
Equation Theory” and solves a system simultaneous equations to determine the support moments - This program contains numerous “comment boxes” which contain a wide variety of information including
explanations of input or output items, equations used, data tables, etc. (Note: presence of a “comment box”
is denoted by a “red triangle” in the upper right-hand corner of a cell. Merely move the mouse pointer to the
desired cell to view the contents of that particular “comment box”.)
Formulas Used to Determine Shear, Moment, Slope, and Deflection in Single-Span Beams
For Uniform or Distributed Loads:
Loading functions for each uniform or distributed load evaluated at distance x = L from left end of beam:
FvL = -wb(L-b-(L-e)) + -1/2(we-wb)/(e-b)((L-b)^2-(L-e)^2)+(we-wb)(L-e)
FmL = -wb/2((L-b)^2-(L-e)^2) + -1/6(we-wb)/(e-b)((L-b)^3-(L-e)^3)+(we-wb)/2(L-e)^2
FqL = -wb/(6EI)((L-b)^3-(L-e)^3) + -1/(24EI)(we-wb)/(e-b)((L-b)^4-(L-e)^4)+(we-wb)/(6EI)(L-e)^3
FDL = -wb/(24EI)((L-b)^4-(L-e)^4) + -1/(120EI)(we-wb)/(e-b)((L-b)^5-(L-e)^5)+(we-wb)/(24EI)(L-e)^4
Loading functions for each uniform or distributed load evaluated at distance = x from left end of beam:
If x >= e:
Fvx = -wb(x-b-(x-e)) + -1/2(we-wb)/(e-b)((x-b)^2-(x-e)^2)+(we-wb)(x-e)
Fmx = -wb/2((x-b)^2-(x-e)^2) + -1/6(we-wb)/(e-b)((x-b)^3-(x-e)^3)+(we-wb)/2(x-e)^2
Fqx = -wb/(6EI)((x-b)^3-(x-e)^3) + -1/(24EI)(we-wb)/(e-b)((x-b)^4-(x-e)^4)+(we-wb)/(6EI)(x-e)^3
FDx = -wb/(24EI)((x-b)^4-(x-e)^4) + -1/(120EI)(we-wb)/(e-b)((x-b)^5-(x-e)^5)+(we-wb)/(24EI)(x-e)^4
else if x >= b:
Fvx = -wb(x-b) + -1/2(we-wb)/(e-b)(x-b)^2 else: Fvx = Fmx = -wb/2(x-b)^2 + -1/6(we-wb)/(e-b)(x-b)^3-(x-e)^3 else: Fmx =
Fqx = -wb/(6EI)(x-b)^3 + -1/(24EI)(we-wb)/(e-b)(x-b)^4 else: Fqx = FDx = -wb/(24EI)(x-b)^4 + -1/(120EI)(we-wb)/(e-b)(x-b)^5 else: FDx =
For Point Loads:
Loading functions for each point load evaluated at distance x = L from left end of beam:
FvL = -P
FmL = -P(L-a) FqL = -P(L-a)^2/(2EI)
FDL = P(L-a)^3/(6E*I)
Loading functions for each point load evaluated at distance = x from left end of beam:
If x > a:
Fvx = -P else: Fvx =
Fmx = -P(x-a) else: Fmx = Fqx = -P(x-a)^2/(2EI) else: Fqx =
FDx = P(x-a)^3/(6E*I) else: FDx =
For Applied Moments:
Loading functions for each applied moment evaluated at distance x = L from left end of beam:
FvL = 0
FmL = -M
FqL = -M(L-c)/(EI)
FDL = M(L-c)^2/(2E*I)
Loading functions for each applied moment evaluated at distance = x from left end of beam:
If x >= c:
Fvx = 0 else: Fvx =
Fmx = -M else: Fmx =
Fqx = -M(x-c)/(EI) else: Fqx =
FDx = M(x-c)^2/(2E*I) else: FDx =
Formulas Used to Determine Shear, Moment, Slope, and Deflection (continued)
Initial summation values at left end (x = 0) for shear, moment, slope, and deflection:
Simple beam:
Vo = -1/L*S(FmL)
Mo = 0
qo = 1/L*S(FDL)+L/(6*E*I)*S(FmL)
Do = 0
Propped beam:
Vo = -3*E*I/L^3*S(FDL)-3*E*I/L^2*S(FqL)
Mo = 0
qo = 3/(2*L)*S(FDL)+1/2*S(FqL)
Do = 0
Fixed beam:
Vo = -12*E*I/L^3*S(FDL)-6*E*I/L^2*S(FqL)
Mo = 6*E*I/L^2*S(FDL)+2*E*I/L*S(FqL)
qo = 0
Do = 0
Cantilever beam:
Vo = 0
Mo = 0
qo = -S(FqL)
Do = -S(FDL)-L*S(FqL) Summations of shear, moment, slope, and deflection at distance = x from left end of beam:
Shear: Vx = Vo+S(Fvx)
Moment: Mx = Mo+Vox+S(Fmx) Slope: qx = qo+Mox/(EI)+Vox^2/(2EI)+S(Fqx)
Deflection: Dx = -(Do-qox-Mox^2/(2EI)-Vox^3/(6E*I)+S(FDx)
Reference:
“Modern Formulas for Statics and Dynamics, A Stress-and-Strain Approach”
by Walter D. Pilkey and Pin Yu Chang, McGraw-Hill Book Company (1978)
“Three-Moment Theory” Used for Continuous-Span Beam Analysis:
The “Three-Moment” Equation is valid for any two (2) consecutive spans as follows:
MaL1/I1+2(Mb)(L1/I1+L2/I2)+McL2/I2
= -6(FEMabL1/(6I1)+FEMbaL1/(3I1))-6(FEMbcL2/(3I2)+FEMcbL2/(6I2))
=-(FEMab+2FEMba)L1/I1-2(FEMbc+FEMcb)L2/I2
where: Ma = internal moment at left support
Mb = internal moment at center support
Mc = internal moment at right support
L1 = length of left span
I1 = moment of inertia for left span
L2 = length of right span
I2 = moment of inertia for right span
FEMab = total Fixed-End-Moment for left end of left span
FEMba = total Fixed-End-Moment for right end of left span
FEMbc = total Fixed-End-Moment for left end of right span
FEMcb = total Fixed-End-Moment for right end of right span
N = actual number of beam spans
Note: “Dummy” spans are used to model the left end and right end support conditions for the beam. A pinned
end is modeled as a very flexible span (very long length and very small inertia). A fixed end is modeled
as a very stiff span (very short length and very large inertia). Thus, the theoretical number of spans used
is = N + 2.
By writing an equation for each pair of consecutive spans and introducing the known values (usually zero)
of end moments, a system of (N+1) x (N+1) simultaneous equations can be set up to solve for the
unknown support moments.
Reference:
AISC Manual of Steel Construction – Allowable Stress Design (ASD) – 9th Edition (1989), page 2-294