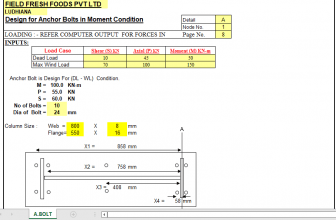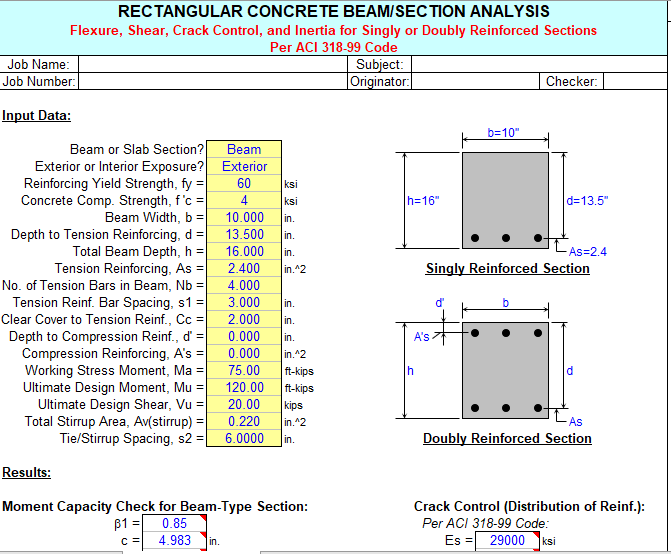
“RECTBEAM” — RECTANGULAR CONCRETE BEAM ANALYSIS/DESIGN
Program Description:
“RECTBEAM” is a spreadsheet program written in MS-Excel for the purpose of analysis/design of rectangular
beam or column sections. Specifically, the required flexural reinforcing, ultimate moment capacity, bar spacing
for crack control, moments of inertia for deflection, beam shear and torsion requirements, and member capacity
for flexure (uniaxial and biaxial) with axial load are calculated. There is also a worksheet which contains
reinforcing bar data tables.
This program is a workbook consisting of eleven (11) worksheets, described as follows:
Worksheet Name Description
Doc This documentation sheet
Complete Analysis Beam flexure, shear, crack control, and inertia
Flexure(As) Flexural reinforcing for singly or doubly reinforced beams/sections
Flexure(Mn) Ultimate moment capacity of singly or doubly reinforced beams/sections
Crack Control Crack control – distribution of flexural reinforcing
Shear Beam or one-way type shear
Torsion Beam torsion and shear
Inertia Moments of inertia of singly or doubly reinforced beams/sections
Uniaxial Combined uniaxial flexure and axial load
Biaxial Combined biaxial flexure and axial load
Rebar Data Reinforcing bar data tables
Program Assumptions and Limitations:
- This program follows the procedures and guidelines of the ACI 318-99 Building Code.
- The “Complete Analysis” worksheet combines the analyses performed by four (4) of the individual
worksheets all into one. This includes member flexural moment capacity, as well as shear, crack control,
and inertia calculations. Thus, any items below pertaining to any of the similar individual worksheets
included in this one are also applicable here. - In the “Flexure(As)” worksheet, the program will display a message if compression reinforcing is required,
when the beam/section cannot handle the ultimate design moment with tension reinforcing only. Then a
doubly-reinforced design is performed. - In the “Flexure(As)” worksheet for a singly reinforced beam/section, when the required flexural reinforcing is
less than the Code minimum, then the program will use the lesser value of either 4/3 times the required value
or the minimum value as the amount to actually use for design. - In the “Flexure(Mn)”, “Uniaxial”, and “Biaxial” worksheets, when the calculated distance to the neutral axis, ‘c’,
is less than the distance to the reinforcement nearest the compression face, the program will ignore that
reinforcing and calculate the ultimate moment capacity based on an assumed singly-reinforced section. - In the “Uniaxial” and “Biaxial” worksheets, the CRSI “Universal Column Formulas” are used by this program
to determine points #1 through #7 of the 10 point interaction curve. - In the “Uniaxial” and “Biaxial” worksheets, the CRSI “Universal Column Formulas”, which are used by this
program, assume the use of the reinforcing yield strength, fy =60 ksi. - In the “Uniaxial” and “Biaxial” worksheets, this program assumes a “short”, non-slender rectangular column
with symmetrically arranged and sized bars. - In the “Uniaxial” and “Biaxial” worksheets, for cases with axial load only (compression or tension) and no
moment(s) the program calculates total reinforcing area as follows:
Ast = (NtbAbt) + (NsbAbs) , where: Abt and Abs = area of one top/bottom and side bar respectively. - In the “Uniaxial” and “Biaxial” worksheets, for pure moment capacity with no axial load, the program assumes
bars in 2 outside faces parallel to axis of bending plus 50% of the total area of the side bars divided equally
by and added to the 2 outside faces, and program calculates reinforcing areas as follows:
for X-axis: As = A’s = ((NtbAbt) + (0.50NsbAbs))/2 for Y-axis: As = A’s = ((NsbAsb+4Atb) + (0.50(Ntb-4)*Atb))/2 - In the “Uniaxial” and “Biaxial” worksheets, design capacities, fPn and fMn, at design eccentricity,
e = Mu*12/Pu, are determined from interpolation within the interaction curve for each axis. - In the “Uniaxial” and “Biaxial” worksheets, when the design eccentricity falls between the “balanced” point
(Point #7) and point of pure flexure (Point #9) the program uses f = 0.7 at Point #7 and f = 0.9 at Point #9.
However, it should be noted that the Code permits the value of ‘f’ to be increased linearly from a starting
value of 0.70 at fPn = 0.1f ‘cAg (Point #8), up to the maximum value of 0.9 at Point #9, using:
f = 0.90 – 2Pu/(f ‘cAg). - In the “Biaxial” worksheet, the biaxial capacity is determined by the following approximations:
a. For Pu >= 0.1f’cAg, use Bresler Reciprocal Load equation:
1/fPn = 1/fPnx + 1/fPny – 1/fPo
Biaxial interaction stress ratio, S.R. = Pu/fPn <= 1
b. For Pu < 0.1f’cAg, use Bresler Load Contour interaction equation:
Biaxial interaction stress ratio, S.R. = (Mux/fMnx)^1.15 + (Muy/fMny)^1.15 <= 1 - The “Rebar Data” worksheet contains tables of reinforcing bar data which include various bar properties,
reinforcing bar areas based on spacing, and various plain welded wire fabric properties. - This program contains numerous “comment boxes” which contain a wide variety of information including
explanations of input or output items, equations used, data tables, etc. (Note: presence of a “comment box”
is denoted by a “red triangle” in the upper right-hand corner of a cell. Merely move the mouse pointer to the
desired cell to view the contents of that particular “comment box”.)